I. Introduction▲
Ce tutoriel va vous aider à comprendre comment ajuster une équation non linéaire à des données. Je ne suis ni mathématicien ni informaticien. Donc, excusez-moi par avance des inexactitudes que je vais écrire, ou des oublis. Par exemple, je ne vais pas définir mes variables dans un certain groupe donné (pardon, les mathématiciens) et mes exemples codés ne seront pas les plus rapides et certainement pas les plus malins (pardon, les programmeurs). Mais, ça marche ! Et c'est le principal. Ce sujet a été traité maintes fois dans plusieurs livres comme cités dans la bibliographie et sur Internet comme sur la page Méthode des moindres carrés de Wikipédia. Je ne prétends pas réinventer la roue, mais juste donner quelques exemples implémentant les sujets discutés ici.
Tout d'abord, je vais supposer que vous savez comment résoudre un système d'équations linéaires. Ceci est très bien expliqué par Jean-Marc Blanc dans son tutoriel intitulé Résolution des systèmes linéaires.
De manière générale, un système d'équations linéaires a un ensemble de solutions exactes, qui peut être trouvé en une étape, par une inversion de matrice ou par l'utilisation de l'opérateur \ dans MATLAB. Afin de rester général, je vais utiliser l'inversion de matrice et la fonction inv. Par exemple, pour trouver l'ensemble des solutions à une droite de la forme :
| (1) |
C'est-à-dire, trouver les solutions ![]() et
et ![]() connaissant une série de
connaissant une série de ![]() mesurés à une « position »
mesurés à une « position » ![]() (où le mot « position » doit être utilisé de manière générale, car pouvant correspondre à une vitesse, un temps, une température…). De manière générale, l'utilisation de la forme matricielle est plus compacte et va donc être utilisée par la suite. Dans ce cas, l'équation (1) devient :
(où le mot « position » doit être utilisé de manière générale, car pouvant correspondre à une vitesse, un temps, une température…). De manière générale, l'utilisation de la forme matricielle est plus compacte et va donc être utilisée par la suite. Dans ce cas, l'équation (1) devient :
| (2) |
Dans cette équation, ![]() correspond aux solutions que l'on veut trouver. Donc ici,
correspond aux solutions que l'on veut trouver. Donc ici, ![]() est un vecteur contenant deux éléments :
est un vecteur contenant deux éléments : ![]() et
et ![]() .
. ![]() est une matrice dont le nombre de colonnes est égal au nombre de variables/solutions (i.e. deux dans notre cas) et dont le nombre de lignes est égal au nombre de points sur la droite (i.e. la taille de
est une matrice dont le nombre de colonnes est égal au nombre de variables/solutions (i.e. deux dans notre cas) et dont le nombre de lignes est égal au nombre de points sur la droite (i.e. la taille de ![]() ). Immédiatement, on peut voir que la première colonne va multiplier le premier élément de
). Immédiatement, on peut voir que la première colonne va multiplier le premier élément de ![]() et la deuxième colonne va multiplier le deuxième élément de
et la deuxième colonne va multiplier le deuxième élément de ![]() . Dans ce cas, si l'on considère que le premier élément de
. Dans ce cas, si l'on considère que le premier élément de ![]() est
est ![]() et le deuxième est
et le deuxième est ![]() , alors la première colonne de
, alors la première colonne de ![]() sera le vecteur unité et la deuxième colonne sera
sera le vecteur unité et la deuxième colonne sera ![]() . Le but est de trouver
. Le but est de trouver![]() :
:
| (3) |
Cependant, l'inversion d'une matrice ne peut se faire que si cette matrice est carrée. Ceci est contourné par l'introduction de la transposée de ![]() qui va être multipliée puis divisée :
qui va être multipliée puis divisée :
| (4) |
On peut écrire dans MATLAB :
function Linear_test
x = [82 ; 271 ; 340.4 ; 431 ; 443.3 ; 516.5 ; 533.6 ; 539.2];
y = [358.5 ; 453.3 ; 488.4 ; 534.1 ; 540.1 ; 576.4 ; 585.2 ; 588.2];
totsize = length(x);
J(1:totsize,1) = ones(totsize,1);
J(1:totsize,2) = x;
solution = inv(J.'*J)*(J.'*y);D'autres méthodes peuvent être utilisées dans MATLAB pour obtenir le même résultat :
solution = J\y;ou :
solution = lscov(J,y);ou encore :
solution = polyfit(x,y,1);Si on avait voulu un ajustement d'ordre 2, il aurait simplement fallu ajouter une troisième colonne à ![]() (
(![]() dont les éléments auraient été
dont les éléments auraient été ![]() et la solution
et la solution ![]() aurait été un vecteur de trois éléments.
aurait été un vecteur de trois éléments.
II. Ajustement non linéaire par la méthode des moindres carrés▲
II-A. Méthode de Gauss-Newton▲
II-A-1. Explication simpliste▲
La méthode de Gauss-Newton consiste à transformer un système d'équations non linéaires en un système d'équations linéaires. Prenons une équation non linéaire ![]() . Elle dépend de deux paramètres
. Elle dépend de deux paramètres ![]() et
et ![]() et est évaluée à divers moments
et est évaluée à divers moments ![]() (où
(où ![]() peut être vu comme une « position » au sens général) :
peut être vu comme une « position » au sens général) : ![]() . Cette fonction devra être minimisée pour n'importe quel
. Cette fonction devra être minimisée pour n'importe quel ![]() ; c'est-à-dire que
; c'est-à-dire que ![]() est implicitement définie comme étant :
est implicitement définie comme étant :
| (5) |
Où ![]() est la fonction s'ajustant aux données expérimentales
est la fonction s'ajustant aux données expérimentales ![]() . Nous supposons que cette équation a un ensemble de solutions, de telle manière que l'on ait le couple de solutions
. Nous supposons que cette équation a un ensemble de solutions, de telle manière que l'on ait le couple de solutions ![]() pour lequel :
pour lequel :
| (6) |
Puis nous développons la fonction en une série de Taylor :
| (7) |
Où ![]() et
et ![]() correspondent aux dérivées partielles
correspondent aux dérivées partielles ![]() et
et ![]() respectivement.
respectivement.
L'équation précédente devient :
| (8) |
Avec ![]() et
et ![]() .
.
De manière générale, ![]() et
et ![]() représentent les paramètres à ajuster de la fonction.
représentent les paramètres à ajuster de la fonction. ![]() et
et ![]() sont des valeurs particulières de
sont des valeurs particulières de ![]() et
et ![]() pour lesquelles la fonction
pour lesquelles la fonction ![]() s'annule.
s'annule.
À ce point, il est important de remarquer plusieurs choses.
Premièrement, la série de Taylor a été tronquée, ce qui signifie que la solution ne peut pas être exacte, mais seulement approximée. À ce titre, la solution devra être trouvée par itérations.
Deuxièmement, nous pouvons alors réécrire ![]() et
et ![]() , où
, où ![]() et
et ![]() sont substitués par
sont substitués par ![]() et
et ![]() respectivement,
respectivement, ![]() désignant la
désignant la ![]() itération.
itération. ![]() et
et ![]() (
(![]() et
et ![]() dans l'équation) sont déjà connus et utilisés. Les seules inconnues sont
dans l'équation) sont déjà connus et utilisés. Les seules inconnues sont ![]() et
et ![]() , qui convergent vers les vraies solutions
, qui convergent vers les vraies solutions ![]() et
et ![]() après plusieurs itérations, en incrémentant à chaque fois
après plusieurs itérations, en incrémentant à chaque fois ![]() et
et ![]() :
: ![]() et
et ![]() .
.
Finalement, l'équation est linéaire et peut donc être résolue très simplement pour ![]() et
et ![]() comme expliqué précédemment.
comme expliqué précédemment.
Il est maintenant nécessaire de généraliser ce que nous avons vu et d'utiliser une formulation matricielle pour le problème. La fonction ![]() est une fonction de deux variables à optimiser évaluée en n points et dépendant du temps
est une fonction de deux variables à optimiser évaluée en n points et dépendant du temps ![]() . Je rappelle ici que les variables sont les coefficients d'une équation et non les points sur l'axe des ordonnées (ici le temps) qui sont connus. On peut alors définir le vecteur :
. Je rappelle ici que les variables sont les coefficients d'une équation et non les points sur l'axe des ordonnées (ici le temps) qui sont connus. On peut alors définir le vecteur :
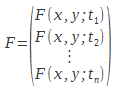 |
(9) |
Le jacobien du système est alors défini par :
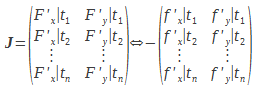 |
(10) |
Le vecteur ![]() permettant l'incrémentation et le vecteur contenant les paramètres :
permettant l'incrémentation et le vecteur contenant les paramètres :
| (11) |
Donc on a :
| (12) |
Il suffit ensuite de répéter ces calculs (calcul de ![]() et de ses dérivées après chaque incrémentation de
et de ses dérivées après chaque incrémentation de ![]() ).
).
Enfin, il faut que l'utilisateur donne les paramètres initiaux que le programme va utiliser comme point de départ pour la minimisation.
II-A-2. Exemple▲
Un exemple de problème d'ajustement non linéaire est donné sur cette page : Algorithme de Gauss-Newton. Le code MATLAB permettant de réaliser l'ajustement est donné ci-dessous.
Les données expérimentales ![]() sont modelées par la fonction :
sont modelées par la fonction :
| (13) |
Les données expérimentales sont connues, de même que ![]() , et il nous faut déterminer les deux paramètres
, et il nous faut déterminer les deux paramètres ![]() et
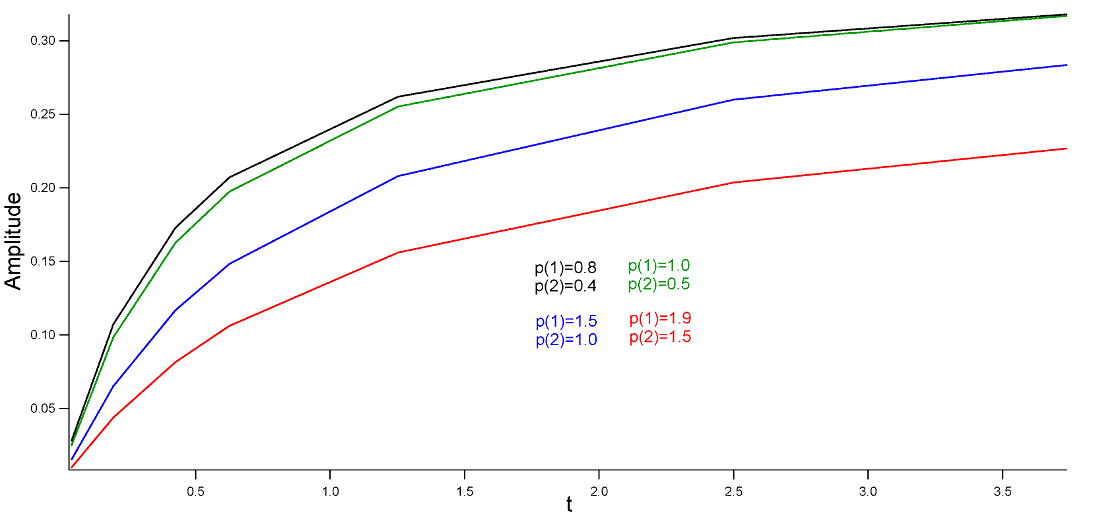
et ![]() pour ajuster au mieux la fonction aux données. La figure suivante montre la fonction à ajuster pour différentes valeurs de ses paramètres.
pour ajuster au mieux la fonction aux données. La figure suivante montre la fonction à ajuster pour différentes valeurs de ses paramètres.
function NewtonMethod
%p est un vecteur de dimension 2x1 contenant les parametres
p(1,1) = 0.8;
p(2,1) = 0.4;
%F = y - (p(1).*t)./(p(2)+t); -> forme de l'equation a minimiser
%dF1 = -t./(p(2)+t); -> forme de la premiere derivee en p(1)
%dF2 = p(1)*x./((p(2)+t).^2); -> forme de la seconde derivee en p(2)
%donnees experimentales
t = [0.038 ; 0.194 ; 0.425 ; 0.626 ; 1.253 ; 2.500 ; 3.740];
D = [0.050 ; 0.127 ; 0.094 ; 0.2122 ; 0.2729 ; 0.2665 ; 0.3317];
%il y aura 5 iterations
for inc = 1:5
%calcul du jacobien
J(1:length(t),1) = -t./(p(2)+t);
J(1:length(t),2) = p(1)*t./((p(2)+t).^2);
%calcul des residus
F = D-(p(1).*t)./(p(2)+t);
%il y a plusieurs manieres de calculer
%l'incrementation Delta
Delta = -inv(J.'*J)*(J.'*F);
%celle-ci est la plus simple sous MATLAB :
%Delta = -J\F;
%incrementation des parametres
p = p+Delta;
end
%calcul de la RMSE
rmse = (sum(F.^2)/length(F))^0.5;
%calcul de l'ecart type (standard deviation)
stdv = (sum(F.^2)/(length(F)-length(p)))^0.5;
%evalutation des donnees ajustees
ta = 0:0.01:4;
Da = (p(1).*ta)./(p(2)+ta);
%affichage des resultats
fprintf('\nB1 = %f\nB2 = %f\n\n', p);
fprintf('rmse = %f\n', rmse);
fprintf('stdv = %f\n\n', stdv);
%affichage du graphique
figure
h = plot(t, D, 'or', ta, Da, 'b');
legend(h, {'Donnees experimentales' 'Meilleur ajustement'}, 'location', 'southeast')
title('Ajustement avec la methode de Gauss-Newton');
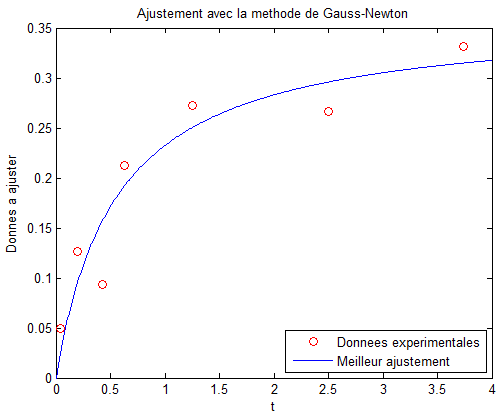
xlabel('t');
ylabel('Donnees a ajuster');Les valeurs calculées sont les suivantes :
B1 = 0.361835
B2 = 0.556256
rmse = 0.033475
stdv = 0.039608Voici un aperçu du graphique avec les données expérimentales et le meilleur ajustement :
II-B. Méthode de Levenberg-Marquardt▲
II-B-1. Explication détaillée▲
Tout d'abord, nous définissons ![]() , un vecteur qui contient tous les paramètres à ajuster. Le
, un vecteur qui contient tous les paramètres à ajuster. Le ![]() paramètre, après
paramètre, après ![]() itérations est défini par :
itérations est défini par :
| (14) |
Si l'on veut ajuster des données expérimentales ![]() à une équation
à une équation ![]() qui dépend de
qui dépend de ![]() (ordonnées),
(ordonnées), ![]() étant la
étant la ![]() donnée, qui sont connues et de paramètres
donnée, qui sont connues et de paramètres ![]() , alors on peut définir la fonction
, alors on peut définir la fonction ![]() par une série de Taylor tronquée à la première dérivée :
par une série de Taylor tronquée à la première dérivée :
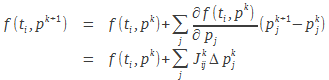 |
(15) |
La quantité à minimiser est le résidu :
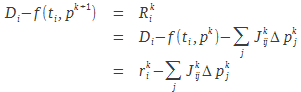 |
(16) |
![]() est un vecteur contenant des résidus, mais obtenu avec les « vieux » paramètres (les seuls auxquels on ait accès à une itération
est un vecteur contenant des résidus, mais obtenu avec les « vieux » paramètres (les seuls auxquels on ait accès à une itération ![]() ). Nous voulons minimiser cette quantité :
). Nous voulons minimiser cette quantité :
| (17) |
Celle-ci représente la somme de toutes les « distances » (qui dépend de l'unité des abscisses) entre les valeurs expérimentales et le modèle. Plus cette valeur est petite et plus le modèle représente au mieux les données. La seule variable dans l'équation (17) est le vecteur ![]() . On dérive donc l'équation (17) par rapport à chaque élément
. On dérive donc l'équation (17) par rapport à chaque élément ![]() et on essaye de trouver
et on essaye de trouver ![]() qui annule la dérivée. Tout d'abord, on peut noter qu'au premier ordre :
qui annule la dérivée. Tout d'abord, on peut noter qu'au premier ordre :
| (18) |
Car les résidus sont supposés représenter le minimum et leurs dérivées s'annulent (bien que ce ne soit pas exactement vrai, surtout lors des premières itérations). Deuxièmement, en notant que ![]() ne dépend pas explicitement de
ne dépend pas explicitement de ![]() , il reste :
, il reste :
| (19) |
Si ![]() , alors
, alors ![]() . Il nous reste donc :
. Il nous reste donc :
| (20) |
Ce qui est équivalent à écrire en termes matriciels :
| (21) |
On voit ici que donner de bons paramètres initiaux est essentiel pour éviter que l'ajustement ne diverge, car la dérivée qui s'annule veut dire que l'on a soit un minimum soit un maximum et il vaut mieux bien sûr que notre algorithme cherche le minimum. Ceci dépend en partie de l'initialisation des paramètres.
L'algorithme de Levenberg-Marquardt consiste en l'introduction d'un terme d'amortissement, ![]() , dans l'équation (21) :
, dans l'équation (21) :
| (22) |
Ce terme permet d'ajuster la fonction en utilisant les caractéristiques de la méthode « steepest-descent » (lorsque les valeurs des paramètres initiaux ![]() sont loin des valeurs finales, avec
sont loin des valeurs finales, avec ![]() large) ou les caractéristiques de la méthode de Gauss-Newton (lorsque
large) ou les caractéristiques de la méthode de Gauss-Newton (lorsque ![]() est proche des valeurs finales, avec
est proche des valeurs finales, avec ![]() petit). Une valeur typique de
petit). Une valeur typique de ![]() pour commencer l'ajustement est
pour commencer l'ajustement est ![]() . Ensuite, la RMSE, pour « root mean square error » (ce terme sera défini avec précision plus loin dans ce tutoriel) doit être calculée plusieurs fois (et donc la fonction elle-même) afin de déterminer la nouvelle valeur de
. Ensuite, la RMSE, pour « root mean square error » (ce terme sera défini avec précision plus loin dans ce tutoriel) doit être calculée plusieurs fois (et donc la fonction elle-même) afin de déterminer la nouvelle valeur de ![]() . À chaque itération, la RMSE est calculée pour
. À chaque itération, la RMSE est calculée pour ![]() et pour
et pour ![]() . Ensuite, à chaque itération, on a les conditions :
. Ensuite, à chaque itération, on a les conditions :
- si
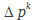 conduit à une moins bonne RMSE que le
conduit à une moins bonne RMSE que le 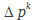 original, alors
original, alors 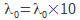 jusqu'à ce qu'une meilleure RMSE soit calculée et le « vieux »
jusqu'à ce qu'une meilleure RMSE soit calculée et le « vieux » 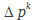 n'est pas remplacé par le nouveau ;
n'est pas remplacé par le nouveau ; - si
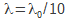 donne la meilleure RMSE, alors
donne la meilleure RMSE, alors 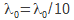 ,
, 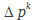 est remplacé et l'itération continue ;
est remplacé et l'itération continue ; - si
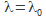 donne la meilleure RMSE, alors on garde
donne la meilleure RMSE, alors on garde 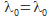 ,
, 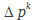 est remplacé et l'itération continue.
est remplacé et l'itération continue.
Bien que cette méthode fasse appel à plus de calculs, elle est stable, en ce sens que les paramètres ![]() , au pire ne convergeront pas, mais dans ce cas, ils ne divergeront pas, car
, au pire ne convergeront pas, mais dans ce cas, ils ne divergeront pas, car ![]() n'est pas recalculé pendant que
n'est pas recalculé pendant que ![]() augmente.
augmente.
II-B-2. Exemple▲
L'exemple précédent est repris, en utilisant la méthode de Levenberg-Marquardt :
function LevenbergMarquardtMethod
%p est un vecteur de dimension 2x1 contenant les parametres
p(1,1) = 0.4;
p(2,1) = 0.2;
%F = y - (p(1).*t)./(p(2)+t); -> forme de l'equation a minimiser
%dF1 = -t./(p(2)+t); -> forme de la premiere derivee en p(1)
%dF2 = p(1)*x./((p(2)+t).^2); -> forme de la seconde derivee en p(2)
%donnees experimentales
t = [0.038 ; 0.194 ; 0.425 ; 0.626 ; 1.253 ; 2.500 ; 3.740];
D = [0.050 ; 0.127 ; 0.094 ; 0.2122 ; 0.2729 ; 0.2665 ; 0.3317];
%initialisation de lambda
lambda0 = 0.01;
rmsea = 15;
rmse = 10;
inc = 0;
%for inc = 1:10
while abs(rmsea-rmse(end))>1e-5 && inc<500 && lambda0 < 1e7
inc = inc+1;
%calcul du jacobien
J(1:length(t),1) = -t./(p(2)+t);
J(1:length(t),2) = p(1)*t./((p(2)+t).^2);
%calcul des residus
F = D-(p(1).*t)./(p(2)+t);
%calul de la RMSE lors de la premiere iteration
if inc==1
rmse = (sum(F.^2)/length(F))^0.5;
else
%mise a jour de lambda
lambda = lambda0;
%generation de la matrice unite
tailleJJ = length(J.'*J);
%calul des delta en fonction de lambda
Delta1 = -inv((J.'*J)+lambda*eye(tailleJJ))*(J.')*F;
lambda=lambda0/10;
Delta2 = -inv((J.'*J)+lambda*eye(tailleJJ))*(J.')*F;
p1 = p;
p2 = p;
%mise a jour des parametres dans un nouveau vecteur
p1 = p1+Delta1;
%calcul des nouveaux residus et de la nouvelle
%RMSE pour lambda=lambda0
F = D-(p1(1).*t)./(p1(2)+t);
rmse1 = (sum(F.^2)/length(F))^0.5;
%calcul des nouveaux residus et de la nouvelle
%RMSE pour lambda=lambda0/10
p2 = p2+Delta2;
F = D-(p2(1).*t)./(p2(2)+t);
rmse2 = (sum(F.^2)/length(F))^0.5;
%condition sur la mise a jour des parametres
%voir texte pour plus de details
if rmse1>rmse && rmse2>rmse
lambda0 = lambda0*10;
elseif rmse2<rmse1
lambda0 = lambda0/10;
p = p2;
rmsea = rmse;
rmse = rmse2;
elseif rmse2>=rmse1
p = p1;
rmsea = rmse;
rmse = rmse1;
end
end
end
%calcul de la RMSE
rmse = (sum(F.^2)/length(F))^0.5;
%calcul de l'ecart type (standard deviation)
stdv = (sum(F.^2)/(length(F)-length(p)))^0.5;
%evalutation des donnees ajustees
ta = 0:0.01:4;
Da = (p(1).*ta)./(p(2)+ta);
%affichage des resultats
fprintf('\np1 = %f\ntp2 = %f\n\n',p);
fprintf('rmse = %f\n',rmse);
fprintf('stdv = %f\n\n',stdv);
%affichage du graphique
figure
h = plot(t, D, 'or', ta, Da, 'b');
legend(h, {'Donnees experimentales' 'Meilleur ajustement'}, 'location', 'southeast')
title('Ajustement avec la methode de Levenberg-Marquardt');
xlabel('t');
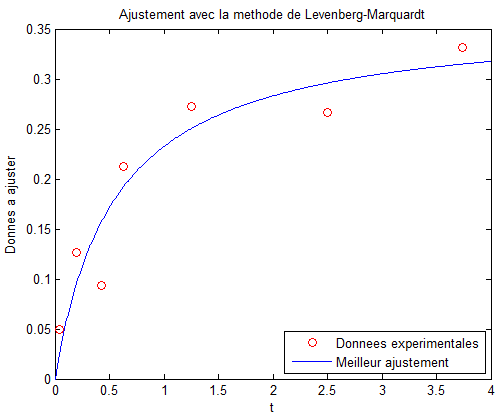
ylabel('Donnees a ajuster');Les valeurs calculées sont les suivantes :
p1 = 0.361697
tp2 = 0.555446
rmse = 0.033475
stdv = 0.039608Voici un aperçu du graphique avec les données expérimentales et le meilleur ajustement :
III. Calcul de quantités statistiques▲
III-A. Qualité d'un ajustement▲
La qualité d'un ajustement peut être évaluée à l'aide de deux critères :
- la racine de la somme des carrés des résidus ou « root mean square error » (RMSE) en anglais ;
- l'écart type ou déviation standard ou encore « standard deviation » en anglais.
III-A-1. Racine de la somme des carrés des résidus ou « root mean square error » (RMSE)▲
La RMSE est la quantité la plus basique, car elle ne dépend que de la distance verticale séparant la donnée expérimentale de la valeur calculée :
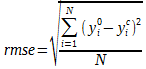 |
(23) |
Où N est le nombre total de points expérimentaux, ![]() est une donnée expérimentale et
est une donnée expérimentale et ![]() est la valeur correspondante calculée. C'est cette valeur qui est minimisée lors du fit.
est la valeur correspondante calculée. C'est cette valeur qui est minimisée lors du fit.
Si l'on prend l'exemple donné au chapitre II.A, le vecteur ![]() (résidu) prend les valeurs [0.0269 0.0334 -0.0627 0.0206 0.0223 -0.0295] duquel on calcule que RMSE=0.033.
(résidu) prend les valeurs [0.0269 0.0334 -0.0627 0.0206 0.0223 -0.0295] duquel on calcule que RMSE=0.033.
III-A-2. Écart type ou « standard deviation »▲
L'écart type est différent de la RMSE en ce sens que l'on prend en compte le nombre de variables ![]() pour modeler les données. L'écart type dépend alors du nombre de degrés de liberté
pour modeler les données. L'écart type dépend alors du nombre de degrés de liberté ![]() :
:
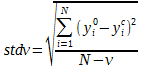 |
(24) |
Où N, ![]() et
et ![]() réfèrent aux mêmes quantités présentées précédemment.
réfèrent aux mêmes quantités présentées précédemment.
Si l'on prend l'exemple donné au chapitre II.A, le vecteur ![]() (résidu) prend les valeurs [0.0269 0.0334 -0.0627 0.0206 0.0223 -0.0295] duquel on calcule que stdv=0.040 avec
(résidu) prend les valeurs [0.0269 0.0334 -0.0627 0.0206 0.0223 -0.0295] duquel on calcule que stdv=0.040 avec ![]() variables.
variables.
III-B. Erreurs sur les données et les paramètres▲
III-B-1. Pondération des données▲
Dans certains cas, une donnée expérimentale peut être déterminée avec une précision moindre que les autres données. Il est alors naturel de vouloir donner moins d'importance à cette donnée dans l'ajustement. Le poids est lié à ![]() représentant l'inverse au carré de l'erreur associée à un point
représentant l'inverse au carré de l'erreur associée à un point ![]() ; et à la variance
; et à la variance ![]() :
:
| (25) |
Où ![]() si
si ![]() et 1 si
et 1 si ![]() ,
, ![]() et
et ![]() représentant l'index des données. Donc
représentant l'index des données. Donc ![]() est une matrice carrée diagonale de taille
est une matrice carrée diagonale de taille ![]() ou
ou ![]() est le nombre total de données expérimentales. Il y a plusieurs manières de déterminer l'erreur dans une donnée expérimentale, mais pour simplifier ici, on suppose qu'elle est proche de la RMSE et nous prenons la valeur 0.035. Habituellement, lorsque je ne connais pas l'erreur avec certitude, je prends
est le nombre total de données expérimentales. Il y a plusieurs manières de déterminer l'erreur dans une donnée expérimentale, mais pour simplifier ici, on suppose qu'elle est proche de la RMSE et nous prenons la valeur 0.035. Habituellement, lorsque je ne connais pas l'erreur avec certitude, je prends ![]() =RMSE;
=RMSE;
La variance est définie par l'équation :
| (26) |
Où ![]() est le nombre de variables utilisées dans le modèle. Si le modèle choisi ajuste les données et que le bruit qui reste est donc gaussien,
est le nombre de variables utilisées dans le modèle. Si le modèle choisi ajuste les données et que le bruit qui reste est donc gaussien, ![]() peut être facilement déterminé et on s'attend à une variance très proche de 1.
peut être facilement déterminé et on s'attend à une variance très proche de 1.
La version pondérée des équations (21) (Gauss-Newton) et (22) (Levenberg-Marquardt) est :
| (27) |
et :
| (28) |
Dans ce cas, la valeur minimisée devient la RMSE pondérée :
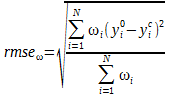 |
(29) |
L'écart type pondéré devient :
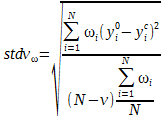 |
(30) |
Il est bon de noter ici que seul le poids relatif des données est important pour la minimisation. Si les poids sont tous les mêmes, alors avoir tous les poids à 5000 ou 1 ne changera rien. Ce qui compte, c'est le poids relatif, c'est-à-dire à quel point les poids sur une ou plusieurs mesures sont différents des autres.
Un exemple d'application de la méthode de Gauss-Newton utilisant la pondération est donné ci-dessous. Ici, c'est la RMSE pondérée qui est minimisée. Pour tester l'algorithme, vous pouvez changer une valeur expérimentale et augmenter fortement l'erreur associée et vérifier que les valeurs finales ne changent que très peu, que la RMSE pondérée reste quasiment inchangée, alors que la RMSE explose.
function NewtonMethod_ponderation
%p est un vecteur de dimension 2x1 contenant les parametres
p(1,1) = 0.8;
p(2,1) = 0.4;
%F = y - (p(1).*t)./(p(2)+t); -> forme de l'equation a minimiser
%dF1 = -t./(p(2)+t); -> forme de la premiere derivee en p(1)
%dF2 = p(1)*x./((p(2)+t).^2); -> forme de la seconde derivee en p(2)
%donnees experimentales
t = [0.038 ; 0.194 ; 0.425 ; 0.626 ; 1.253 ; 2.500 ; 3.740];
D = [0.050 ; 0.127 ; 0.094 ; 0.2122 ; 0.2729 ; 0.2665 ; 0.3317];
%ponderation
weight = [0.03 0.05 0.03 0.04 0.03 0.03 0.06];
w = eye(length(t));
w(w~=0) = 1./(weight.^2);
%il y aura 5 iterations
for inc = 1:5
%calcul du jacobien
J(1:length(t),1) = -t./(p(2)+t);
J(1:length(t),2) = p(1)*t./((p(2)+t).^2);
%calcul des residus
F = D-(p(1).*t)./(p(2)+t);
%calcul de la variance
variance2 = sum(((F.^2).')./(weight.^2))./(length(t)-length(p));
%calul de la matrice de ponderation
w = variance2*w;
%il y a plusieurs manieres de calculer l'incrementation Delta
Delta = -inv(J.'*w*J)*(J.'*w*F);
%incrementation des parametres
p = p+Delta;
%retour à la matrice de ponderation
w = w/variance2;
end
%calcul de la RMSE
rmse = (sum(F.^2)/length(F))^0.5;
%calcul de la RMSE ponderee
rmsew = (sum(diag(w).*(F.^2))/sum(diag(w)))^0.5;
%calcul de l'ecart type (standard deviation)
stdv = (sum(F.^2)/(length(F)-length(p)))^0.5;
%evalutation des donnees ajustees
ta = 0:0.01:4;
Da = (p(1).*ta)./(p(2)+ta);
%affichage des resultats
fprintf('\nB1 = %f\nB2 = %f\n\n',p);
fprintf('rmse = %f\n',rmse);
fprintf('rmsew = %f\n',rmsew);
fprintf('stdv = %f\n\n',stdv);
%affichage du graphique
figure
h = plot(t, D, 'or', ta, Da, 'b');
legend(h, {'Donnees experimentales' 'Meilleur ajustement'}, 'location', 'southeast')
title('Ajustement avec la methode de Gauss-Newton et ponderation');
xlabel('t');
ylabel('Donnees a ajuster');Les valeurs calculées sont les suivantes :
B1 = 0.361939
B2 = 0.625569
rmse = 0.034376
rmsew = 0.035185
stdv = 0.040675Voici un aperçu du graphique avec les données expérimentales et le meilleur ajustement :
III-B-2. Erreurs sur les paramètres - Matrice de corrélation▲
Avant de rentrer dans le vif du sujet, il est important de prendre conscience que les calculs qui suivent et qui permettent d'évaluer l'erreur sur les paramètres ne sont valides que si et seulement si la fonction est appropriée pour décrire les données. C'est-à-dire que si la fonction n'est pas appropriée, alors les paramètres n'auront pas de sens et encore moins l'erreur sur les paramètres. De plus, les erreurs systématiques, souvent très dures à trouver (car cachées et donc non détectées), ne sont pas prises en compte. En gros, ces erreurs n'ont de sens que si le bruit est supposé gaussien et donc aléatoire. Finalement, l'autre point à noter est que pour que les paramètres aient du sens, il faut généralement avoir assez de points par paramètre. Généralement, une valeur de dix points par paramètre (ou plus) est suffisante pour que l'erreur donnée corresponde à 1![]() ou une déviation standard, ou bien il faut que le nombre de degrés de liberté soit large (
ou une déviation standard, ou bien il faut que le nombre de degrés de liberté soit large (![]() , en rappelant que le nombre de degrés de liberté est défini par
, en rappelant que le nombre de degrés de liberté est défini par ![]() ). Je vais continuer à utiliser le même modèle avec les mêmes données, pour assurer une continuité entre les divers chapitres de cet article, mais sachez que je n'ai pas assez de points par paramètre pour m'assurer que le vrai paramètre est contenu dans
). Je vais continuer à utiliser le même modèle avec les mêmes données, pour assurer une continuité entre les divers chapitres de cet article, mais sachez que je n'ai pas assez de points par paramètre pour m'assurer que le vrai paramètre est contenu dans ![]() à 68,3 %.
à 68,3 %.
L'équation permettant de calculer la déviation standard pour chaque paramètre est :
| (31) |
Où ![]() est un vecteur de même dimension que le nombre de paramètres, contenant les déviations standards de chaque paramètre, rangées dans le même ordre que dans le jacobien.
est un vecteur de même dimension que le nombre de paramètres, contenant les déviations standards de chaque paramètre, rangées dans le même ordre que dans le jacobien. ![]() est définie dans l'équation (26). On retrouve ici la matrice de pondération
est définie dans l'équation (26). On retrouve ici la matrice de pondération ![]() . On peut voir ici toute son importance, car les erreurs sur les paramètres dépendent directement des incertitudes liées aux mesures. Alors que dans les équations (27) et (28), seul le poids relatif de chaque mesure par rapport aux autres est important, le poids absolu devient critique pour bien calculer l'erreur associée à chaque paramètre. Personnellement, j'affiche toujours la valeur
. On peut voir ici toute son importance, car les erreurs sur les paramètres dépendent directement des incertitudes liées aux mesures. Alors que dans les équations (27) et (28), seul le poids relatif de chaque mesure par rapport aux autres est important, le poids absolu devient critique pour bien calculer l'erreur associée à chaque paramètre. Personnellement, j'affiche toujours la valeur ![]() , qui me dit combien de fois mon paramètre est plus grand que sa déviation standard. Dans le cas où ce nombre est inférieur à 1, cela veut dire que l'erreur sur mon paramètre est plus grande que le paramètre lui-même, une indication que ce paramètre n'est sûrement pas utile ou approprié dans le modèle utilisé, ou encore qu'il n'y a pas assez de données pour le caractériser.
, qui me dit combien de fois mon paramètre est plus grand que sa déviation standard. Dans le cas où ce nombre est inférieur à 1, cela veut dire que l'erreur sur mon paramètre est plus grande que le paramètre lui-même, une indication que ce paramètre n'est sûrement pas utile ou approprié dans le modèle utilisé, ou encore qu'il n'y a pas assez de données pour le caractériser.
La matrice de covariance, de taille ![]() est calculée de manière très similaire, en utilisant l'équation :
est calculée de manière très similaire, en utilisant l'équation :
| (32) |
De laquelle on tire la matrice de corrélation :
| (33) |
On peut voir que toutes ces matrices et valeurs dépendent du jacobien, qui représente les dérivées de la fonction s'ajustant aux données. La matrice de covariance permet de déterminer les relations entre paramètres, c'est-à-dire, de quelle manière un paramètre ![]() va être affecté si je change la valeur d'un paramètre
va être affecté si je change la valeur d'un paramètre ![]() (en le fixant), tout en continuant d'essayer de minimiser mes données. Est-ce que le paramètre
(en le fixant), tout en continuant d'essayer de minimiser mes données. Est-ce que le paramètre ![]() est très dépendant de la valeur que le paramètre
est très dépendant de la valeur que le paramètre ![]() va prendre ? Par exemple, est-ce qu'un terme constant introduit pour corriger un éventuel décalage (offset) des données est important pour déterminer les paramètres déterminant la courbe des données ? Intuitivement, la réponse est non. La matrice de corrélation est la matrice de covariance normalisée, pour pouvoir discuter des dépendances entre les divers paramètres. Dans l'idéal, on veut des dépendances minimales entre paramètres, pour que les solutions soient le plus orthogonales possible et éviter d'avoir des paramètres qui vont être en compétition pour représenter une même caractéristique de la courbe à ajuster. Par exemple, essayer de modéliser une gaussienne avec un terme quadratique d'ajustement de la ligne de base est dangereux, car le terme quadratique peut essayer de partiellement s'ajuster à la gaussienne (si celle-ci est bruitée par exemple), ce qui aura une incidence sur la valeur finale des paramètres décrivant la gaussienne. Une forte corrélation entre un ou plusieurs paramètres de la gaussienne et ce terme quadratique est alors attendue.
va prendre ? Par exemple, est-ce qu'un terme constant introduit pour corriger un éventuel décalage (offset) des données est important pour déterminer les paramètres déterminant la courbe des données ? Intuitivement, la réponse est non. La matrice de corrélation est la matrice de covariance normalisée, pour pouvoir discuter des dépendances entre les divers paramètres. Dans l'idéal, on veut des dépendances minimales entre paramètres, pour que les solutions soient le plus orthogonales possible et éviter d'avoir des paramètres qui vont être en compétition pour représenter une même caractéristique de la courbe à ajuster. Par exemple, essayer de modéliser une gaussienne avec un terme quadratique d'ajustement de la ligne de base est dangereux, car le terme quadratique peut essayer de partiellement s'ajuster à la gaussienne (si celle-ci est bruitée par exemple), ce qui aura une incidence sur la valeur finale des paramètres décrivant la gaussienne. Une forte corrélation entre un ou plusieurs paramètres de la gaussienne et ce terme quadratique est alors attendue.
Les paramètres et les erreurs sont généralement affichés en donnant la valeur du paramètre puis la déviation standard, entre parenthèses, là où s'arrête le dernier chiffre significatif. Voici un exemple provenant directement du code MATLAB donné ci-après. ![]() et
et ![]() . On peut alors écrire
. On peut alors écrire ![]() ou
ou ![]() ce qui signifie
ce qui signifie ![]() et
et ![]() respectivement. Pour les deux autres paramètres (
respectivement. Pour les deux autres paramètres (![]() ,
, ![]() ,
, ![]() et
et ![]() ), on aurait
), on aurait ![]() et
et ![]() . Certaines personnes donnent les paramètres avec
. Certaines personnes donnent les paramètres avec ![]() (la confiance dans l'intervalle donné étant alors de 95,5 %).
(la confiance dans l'intervalle donné étant alors de 95,5 %).
Les diverses quantités introduites dans ce chapitre sont calculées dans l'exemple de code ci-dessous. Un décalage a été ajouté sur les données expérimentales ![]() et le modèle a été ajusté pour prendre en compte ce changement. Le modèle est donc maintenant :
et le modèle a été ajusté pour prendre en compte ce changement. Le modèle est donc maintenant : ![]() .
.
function NewtonMethod_ponderation_error_parameters
%p est un vecteur de dimension 3x1 contenant les parametres
p(1,1) = 0.8;
p(2,1) = 0.4;
p(3,1) = 0.5;
%F = y - (p(1).*t)./(p(2)+t); -> forme de l'equation a minimiser
%dF1 = -t./(p(2)+t); -> forme de la premiere derivee en p(1)
%dF2 = p(1)*x./((p(2)+t).^2); -> forme de la seconde derivee en p(2)
%donnees experimentales
t = [0.038 ; 0.194 ; 0.425 ; 0.626 ; 1.253 ; 2.500 ; 3.740];
D = [0.050 ; 0.127 ; 0.094 ; 0.2122 ; 0.2729 ; 0.2665 ; 0.3317];
D = D + 0.57;
weight = [0.03 0.02 0.035 0.05 0.04 0.035 0.07];
w = eye(length(t));
w(w~=0) = 1./(weight.^2);
%il y aura 10 iterations
for inc = 1:5
%calcul du jacobien
J(1:length(t),1) = -t./(p(2)+t);
J(1:length(t),2) = p(1)*t./((p(2)+t).^2);
J(1:length(t),3) = -ones(1,length(t));
%calcul des residus
F = D-((p(1).*t)./(p(2)+t)+p(3));
%calcul de la variance
variance2 = sum(((F.^2).')./(weight.^2))./(length(t)-length(p));
%calul de la matrice de ponderation
w = variance2*w;
%il y a plusieurs manieres de calculer
%l'incrementation Delta
Delta = -inv(J.'*w*J)*(J.'*w*F);
%incrementation des parametres
p = p+Delta;
w = w/variance2;
end
%Deviation standard des parametres
stdp = sqrt(variance2)*diag(sqrt((inv((J.')*w*J))));
%Parametres divises par stdp
p_stdp = p./stdp;
%Calcul de la matrice variance-covariance pour calculer
%la matrice de correlation qui va etre affichee a l'ecran.
%La matrice est symetrique et seulement une moitie doit etre calculee.
covmat = sqrt(variance2)*inv(J.'*w*J);
for inc = 1:3
for tt = 1:inc
CorrelationMatrix(inc,tt) = covmat(inc,tt)/sqrt(covmat(inc,inc)*covmat(tt,tt));
end
end
%calcul de la RMSE
rmse = (sum(F.^2)/length(F))^(0.5);
%calcul de la RMSE ponderee
rmsew = (sum(diag(w).*(F.^2))/sum(diag(w)))^0.5;
%calcul de l'ecart type (standard deviation)
stdv = (sum(F.^2)/(length(F)-length(p)))^(0.5);
%evalutation des donnees ajustees
ta = 0:0.01:4;
Da = (p(1).*ta)./(p(2)+ta) + p(3);
%affichage des resultats
fprintf('\np1 = %f\np2 = %f\np3 = %f\n\n',p);
fprintf('error_p1 = %f\nerror_p2 = %f\nerror_p3 = %f\n\n',stdp);
fprintf('p1_stdp1 = %f\np2_stdp2 = %f\np3_stdp3 = %f\n\n',p_stdp);
fprintf(' p(1) p(2) p(3)');
for inc = 1:3
fprintf('\np(%d)\t', inc);
for tt = 1:inc
fprintf(' %4.3f\t',CorrelationMatrix(inc,tt));
end
end
fprintf('\n\n');
fprintf('rmse = %f\n',rmse);
fprintf('rmsew = %f\n',rmsew);
fprintf('stdv = %f\n\n',stdv);
figure
h = plot(t, D, 'or', ta, Da, 'b');
legend(h, {'Donnees experimentales' 'Meilleur ajustement'}, 'location', 'southeast')
title({'Ajustement avec la methode de Gauss-Newton' 'avec calcul des erreurs sur les parametres'});
xlabel('t');
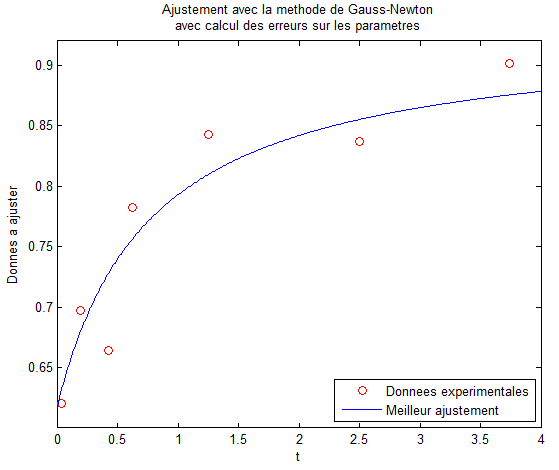
ylabel('Donnees a ajuster');Les valeurs calculées sont les suivantes :
p1 = 0.311792
p2 = 0.774445
p3 = 0.617076
error_p1 = 0.074810
error_p2 = 0.726572
error_p3 = 0.041097
p1_stdp1 = 4.167804
p2_stdp2 = 1.065890
p3_stdp3 = 15.015118
p(1) p(2) p(3)
p(1) 1.000
p(2) 0.604 1.000
p(3) 0.085 0.793 1.000
rmse = 0.032253
rmsew = 0.029378
stdv = 0.042667Voici un aperçu du graphique avec les données expérimentales et le meilleur ajustement :
IV. Conclusion▲
J'espère que cet article pourra vous être utile pour commencer à faire des ajustements non linéaires par vous-même, ou au moins vous aider à y voir plus clair sur ce que qui se passe lors d'une minimisation. Les méthodes proposées sont parmi les plus communément utilisées pour faire des ajustements linéaires : méthode de Gauss-Newton et de Levenberg-Marquardt. L'utilisation de la pondération permet de mieux traiter les données en minimisant l'importance de celles qui sont les plus bruitées. Enfin, les calculs de la RMSE (pondérée ou non), de la déviation standard (pondérée ou non) ainsi que l'erreur sur les paramètres, permettent de déterminer la qualité de l'ajustement. Tout ceci mis bout à bout permet d'effectuer une analyse complète de données par un ajustement non linéaire.
Bien sûr, je ne suis pas à l'abri des erreurs et si vous en voyez. N'hésitez pas à me contacter pour me dire ce qui ne va pas !
Vos remarques et corrections sont les bienvenues dans cette discussion 3 commentaires ![]()
Il reste encore bien des sujets à couvrir, comme coder des simplexes (qui ne font pas appel à des dérivées), ou la minimisation orthogonale, qui pourront s'ajouter à ce tutoriel, mais plus tard.
Voilà, bon courage dans le monde de la minimisation !
V. Bibliographie▲
Voici quelques liens qui vous permettront d'approfondir le sujet développé dans ce tutoriel :
- Algorithme de Gauss-NewtonAlgorithme de Gauss-Newton et méthode des moindres carrés sur Wikipédia ;
- G. Wheatley, Applied Numerical Analysis, Pearson Education, Inc., 2004 ;
- H. Lefebvre-Brion and R. W. Field, The Spectra and Dynamics of Diatomic Molecules, Elsevier Academic Press, 2004.
VI. Remerciements▲
Je remercie Dut pour l'aide apportée pendant la rédaction de ce tutoriel ainsi que ClaudeLELOUP pour ses corrections orthographiques.